Today's box is Blue, another Easy Windows box. The REAL challenge here was user, on my part. In the end, I wound up trying to use the wrong version of Python to run the exploit. :S But I have to admit, it was kina fun using a leaked NSA exploit!
The name kinda suggests that we'll be using the EternalBlue vulnerability, but we might be getting ahead of ourselves; we still have to enumerate from the start like we don't know what is going on.
A quick port scan shows us we're dealing with some Windows Shares (Samba/SMB/CIFS), further supporting EternalBlue. A complete port scan shows a few more ports, but they all relate to SMB, adding more support to EternalBlue, but we need to validate, not just guess... Fortunately, nmap has a scan builtin, and a quick check shows us that it is indeed Vulnerable to EternalBlue:
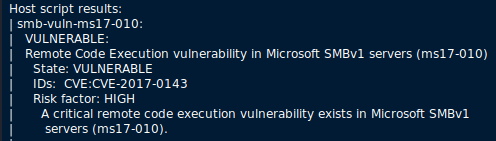
So my hunch was correct. Now to exploit this!
A quick Google seach shows that this is very easily done with Metasploit, but since I want to try to keep the commands and processes all OSCP-friendly, we can't take that (really) easy route. So on to finding a more... "manual" exploit.
Turns out we have to use "Fuzzbunch", one of the tools leaked by the Shadow Brokers from the NSA!? Using the instructions found here, we need to install Fuzzbunch.
And after a couple hours wasted time, I can't Fuzzbunch to actualy exploit. It runs and all, but the exploit itself always fails. So maybe Fuzzbunch isn't the right option. Maybe I gotta take another step back...
Several Google searches, many more false rabbit holes, and a few hours later... maybe I'm just overcomplicating this.
So let's take another look at searchsploit on kali, and we see there's a couple of "built-in" options that may work, most notably, 42315.py. So copy that to our HTB directory and take a deeper look at the code in a text editor.
After much work and effort, I am very reasonably sure that this IS the exploit and process to use, but I keep getting all kinds of Python errors in my Kali setup.
Eventually, I stumbled across this page while serching for how to manually exploit EternalBlue:
https://ivanitlearning.wordpress.com/2019/02/24/exploiting-ms17-010-without-metasploit-win-xp-sp3/
A few hours later... DO NOT USE PYTHON3, USE PYTHON!
I had started to give up hope that *I* would be able to accomplish this one... but on a bit of a whim, I decided to install python-pip (instead of relying on pip3), installed impacket with pip (NOT pip3), and BOOM! IT WORKED!
Fortunately, as soon as the exploit worked, it got us full Admin access, so we didn't need to escalate our privileges (this time).
Report for HackTheBox Blue |
|
 Thursday, 06 August 2020 15:50 Thursday, 06 August 2020 15:50  133.19 KB 133.19 KB  517 517 |
Download |
Sadly, due to the amount of time wasted trying to run the wrong version of Python (SO embarassing :S ), I can't get the report as prettied up as I would during my self-imposed time limits, so we'll just have to put it out as-is, and get on to the next!

